cs231n PPT与笔记

0.学习资源

2023.04.16

1. 视频

2. 官方课程笔记

3. 课程笔记中文翻译

4. ConvNetJS

5. ppt

6. gcloud

1. 工具

python

教程：https://cs231n.github.io/python-numpy-tutorial/

看完这个就好了 Colab:google 版的 Jupyter Notebook

基于数据驱动

线性分类器：f(x,W) = Wx + b

损失函数：

1. 需要一个度量W好坏的方法，可以用一个函数把W当作输入，看一下得分，定量估计W的好坏，这个函数被称为损失函数。
2. 将权重w衡量权重好坏的函数叫损失函数* loss function

python:

1
2
3
4
5
6

def L_i_vectorized(x,y,W):
    scores = W.dot(x)
    margins = np.maximum(0, scores - scores[y] + 1)
    margins[y] = 0
    loss_i = np.sum(margins)
    return loss_i

正则项：（惩罚模型的复杂性，提高模型泛化能力）

1. 绿色线是我们更希望看到的。
2. 正则化惩罚项 lamdaR ,lamda是超参数。使得没有加入惩罚项之前的W拟合出来的过拟合的曲线，我们更希望看到的是直线，这样在测试集上也能用。主要目的是减轻模型的复杂程度，而不是去试图过拟合数据。
3. L2正则项目是对这个权重向量W的欧式范数进行惩罚
4. 同理，L1正则项是对权重向量W的L1范数进行惩罚

SoftMax 分类器

1. 所有类别的概率和为1

Softmax vs. SVM

两个损失函数的区别是：

1. svm关心的是正确分类的分值和不正确分类的分值的边际
2. softmax或者交叉熵损失，我们计算一个概率分布，然后查看正确分类负对数的概率。

优化 Optimization

通过损失函数求最优参数W

1. 梯度就是偏导数组组成的向量，指向函数增加最快的方向，负方向指向函数下降最快的方向。
2. 使用梯度更新参数向量。

Gradient Descent：

1
2
3

while True:
    weights_grad = evaluate_gradient(loss_fun,data,weights) # weights 预先随机化为初值
    weights + = -setp_size * weights_grad

步长step_size 是超参数（学习率learning rate）

步长国小有可能2陷入局部最优解。

Stochastic Gradient Descent 随机梯度下降

1
2
3
4

while True：
	data_batch = sample_training_data(data,256)#sample 256 examples
    weights_grad = evaluate_gradient(loss_fun, data_batch, weights)
    weights += -steps_size*weights_grad #perform parameter update

batch（minibatch） 一般大小为32 64 128，使用minbatch来估算总误差和以及实际梯度

Aside:Image Features

two stage:

1. 计算特征，将不同特征合起来得到图像的特征表述
2. 将这些特征表述作为输入源传入线性分类器

反向传播

计算图(帮助你更好地理解BP)


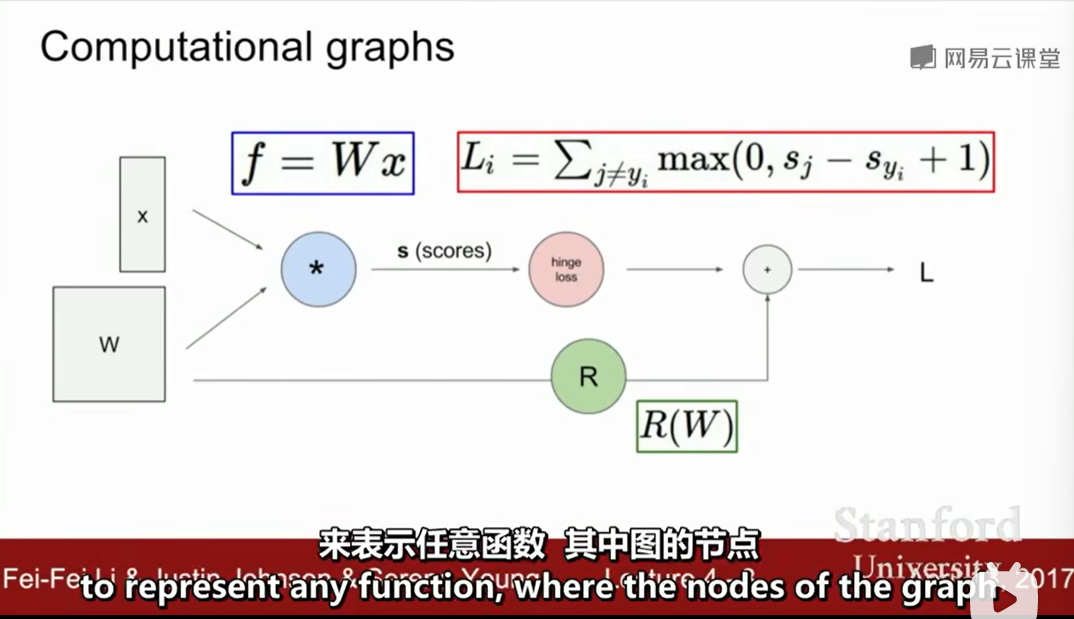
hinge loss: 计算数据损失项Li

现在想求x，y，z的偏导数，绿色为输入值，红色为反向链式计算出来的梯度值

上面例子df/dy = -4，使用链式法则就能求出想要的梯度值

反向传播就是在计算图上用链式法则求梯度，用于更新W。

上面的流程就是输入绿色的输入值，前向传播得到最终的L。

然后反向传播计算的到一层一层的梯度值。

sigmoid 求偏导是上面df(x)/dx将结果0.73代入到该点灯饰得到梯度为(1-0.73)*0,73 = 0.2

当一个节点的输入是一个向量，权重是矩阵时

Graph(or Net)object (rough psuedo code)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

![activationfunctions](D:\Blogs\littlebear_hexoblog\source\_posts\MAD_Learning\cs231nNotes\activationfunctions.png)class ComputationalGraph(object):
    #...
    def forward(inputs):
        # 1.[pass inputs to gates...]
        # 2.forward the computational graph:
        for gate in self.graph.nodes_topologically_sorted():
            gate.forward()
        return loss # the final gate in the graph outputs the loss
    def backward():
        for gate in reversed(self.graph.nodes_topologically_sorted()):
            gate.backward() # little piece of backprop(chain rule applied)
        return inputes_gradients
    
class MultiplyGate(object):
    def forward(x, y):
        z = x*y
        self.x = x # must keep these around!
        self.y = y
        return z
    def backward(dz):
        dx = self.y * dz # [dz/dx * dL/dz]
        dy = self.x * dz # [dz/dy * dL/dz]
       	return [dx, dy]

神经网络

激活函数

激活函数以及作用

问题一：为什么我们要使用激活函数呢？

如果不使用激活函数，我们的每一层输出只是承接了上一层输入函数的线性变换，无论神经网络有 多少层，输出都是输入的线性组合。如果使用的话，激活函数给神经元引入了非线性的因素，使得神经网络可以逼近任何非线性函数，这样神经网络就可以应用到非线性模型中。

问题二：那么为什么我们需要非线性函数？

非线性函数是那些一级以上的函数，而且当绘制非线性函数时它们具有曲率。现在我们需要一个可以学习和表示几乎任何东西的神经网络模型，以及可以将输入映射到输出的任意复杂函数。神经网络被认为是通用函数近似器（Universal Function Approximators）。这意味着他们可以计算和学习任何函数。几乎我们可以想到的任何过程都可以表示为神经网络中的函数计算。

问题三：如何选择激活函数？

1、sigmoid 激活函数：除了输出层是一个二分类问题基本不会用它。

2、tanh 激活函数： tanh 是非常优秀的， 几乎适合所有场合。

3、ReLu 激活函数：最常用的默认函数，如果不确定用哪个激活函数，就使用 ReLu 或者Leaky ReLu。

全连接层

神经网络

卷积神经网络历史

卷积和池化

卷积

1. 卷积可以保持输入的形状
2. 一个卷积核就可以得到一层激活映射，六个卷积核就可以得到六层激活映射
3. 卷积层越深，特征越复杂

1. 第一层卷积层Conv1，这些网格中每个部分都是神经元，这里可视化是这个输入长什么样子它将特定神经元的激活函数最大化，输入什么长什么样子使得神经元拥有最大值。表示的是神经元寻找使得他们最大化的图像。

input image，经过卷积层，经过非线性层（一般是Relu），经过池化层……经过全连接层连接所有的卷积输出 ，最终获得一个最终的分值函数。

这些措施大大降低了激活映射的采样尺寸。

0 padding 的作用是当stride是1的时候，保持输入的大小，以及在边角区域应用卷积核。

需要处理的图像是多层叠在一起的，如果不做 0 padding，或任何形式的填充，输出图像会迅速减小，这回损失一些信息，你只能用很少的值

一个卷积层的参数量计算：

stride的选择：是否降采样

池化

图像中的相邻像素倾向于具有相似的值，因此通常卷积层相邻的输出像素也具有相似的值。这意味着，卷积层输出中包含的大部分信息都是冗余的。

如果我们使用边缘检测滤波器并在某个位置找到强边缘，那么我们也可能会在距离这个像素1个偏移的位置找到相对较强的边缘。但是它们都一样是边缘，我们并没有找到任何新东西。

池化层解决了这个问题。这个网络层所做的就是通过减小输入的大小降低输出值的数量。

池化一般通过简单的最大值、最小值或平均值操作完成。以下是池大小为2的最大池层的示例:

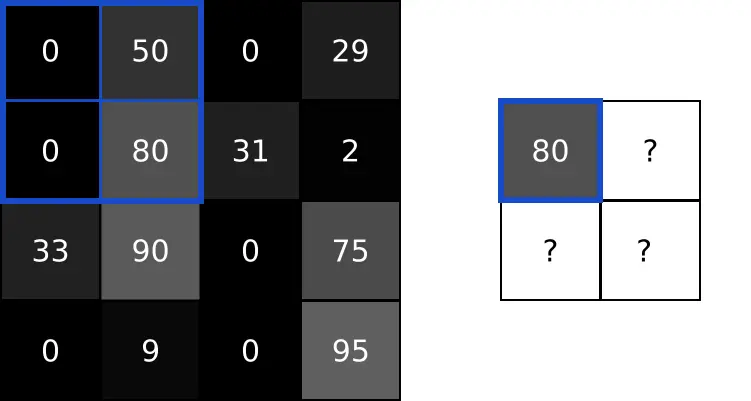
视觉之外的卷积神经网络


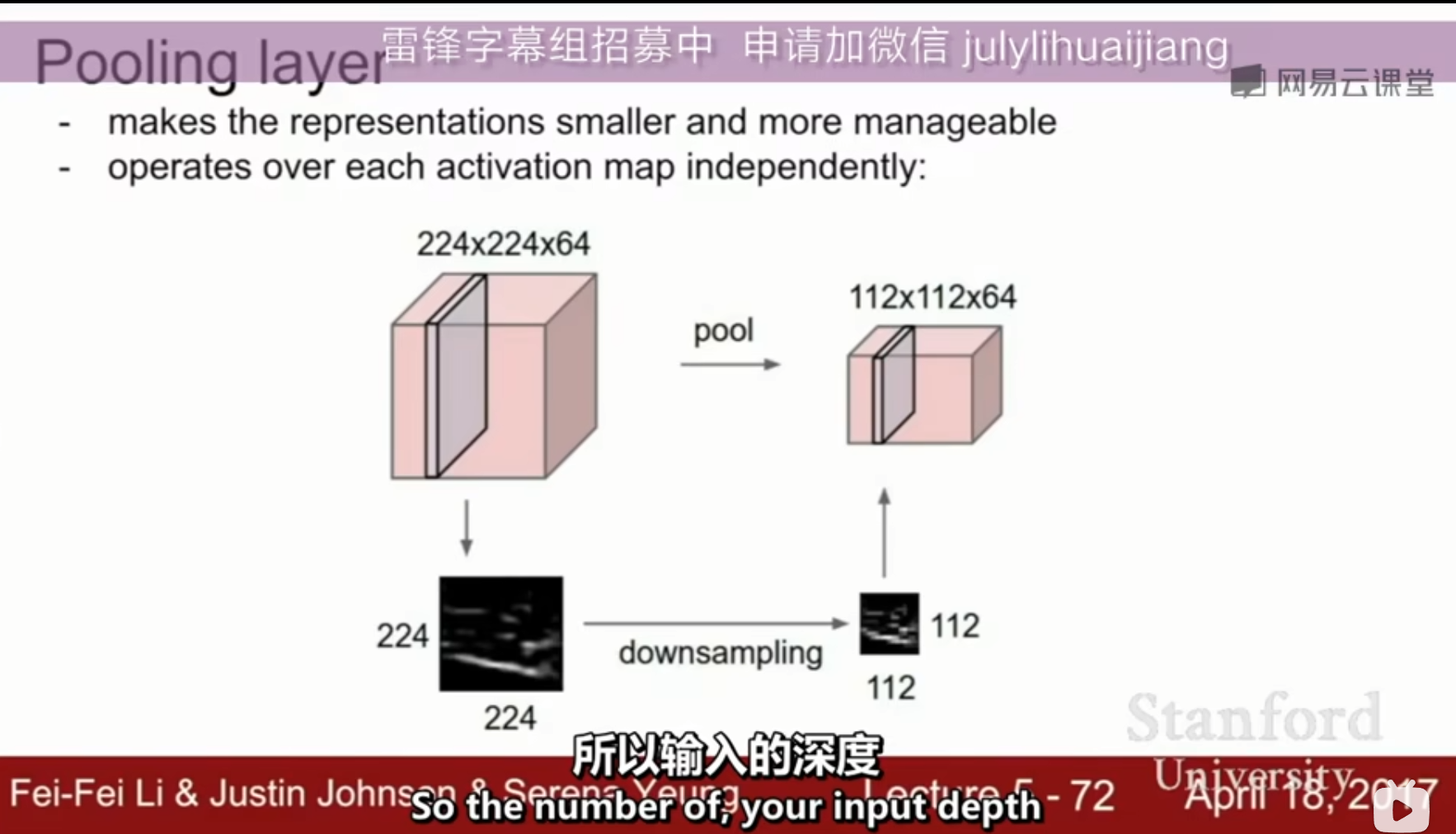
1. pooling 类似于下采样

2. 通常使用的 是max pooling，也会使用stride进行下采样

3. pooling不会进行padding，因为本身就是在下采样没必要做保持输出大小的padding操作

全连接层

https://zhuanlan.zhihu.com/p/33841176

在最后不在需要保全之前的空间结构了，而在最后一层把所有的内容汇聚到一起，我们想根据这些信息得到一些结论（score output）

训练神经网络

激活函数

介绍

sigmoid：

1. 当输入很大或者很小的时候，饱和的神禁苑会造成梯度会消失，将无法得到梯度流的反馈，当输入接近于0的时候会得到比较好的梯度。

2. sigmoid函数是非0中心函数这种情况梯度更新效率会非常低。

   不是0均值（zero-centered）的，这会导致后层的神经元的输入是非0均值的信号，这会对梯度产生影响。以 f=sigmoid(wx+b)为例， 假设输入均为正数（或负数），那么对w的导数总是正数（或负数），这样在反向传播过程中要么都往正方向更新，要么都往负方向更新，导致有一种捆绑效果，使得收敛缓慢。

3. 使用了指数函数，计算代价有点高。

优点:

ReLu的收敛速度比 sigmoid 和 tanh 快；
输入为正时，解决了梯度消失的问题，适合用于反向传播。；
计算复杂度低，不需要进行指数运算；
缺点:

ReLU的输出不是zero-centered；
ReLU不会对数据做幅度压缩，所以数据的幅度会随着模型层数的增加不断扩张。(有下界无上界)
Dead ReLU Problem（神经元坏死现象）：x为负数时，梯度都是0，这些神经元可能永远不会被激活，导致相应参数永远不会被更新。（输入为负时，函数存在梯度消失的现象）

1. 为了防止Relu函数不被激活，让更多的Relus在一开始就能放电的偏置项（0.01），可能有用可能没用。

leaky ReLU

PReLU

ELU 负饱和

批量归一化

不同的评价指标往往具有不同的量纲和量纲单位，这样无法对结果进行分析，难以对结果进行衡量，为了消除指标之间的量纲影响，需要对数据进行标准化处理，以使数据指标之间存在可比性。

归一化：是指变量减去它的均值，再除以标准差；

优点：归一化后加快了梯度下降求最优解的速度；并且有可能提高精度。

图像在大部分情况下，我们的确会做零中心化的处理，但实际上我们不会真的过多地归一化像素值，因为一般对图像来说，在每个位置你已经得到了相对可比较地范围与分布，所以我们没必要归一化太多。（一般是在机器学习里面，这些特征会处于的范围差别特别大）

图像零中心处理：

零均值化：是指变量减去它的均值；

优点：在反向传播时加快网络中每层权重参数的收敛；还可以增加基向量的正交性。

为了加快收敛

在训练阶段，我们会决定我们的均值。然后会将一样的均值应用到测试数据中去。所以我们会从训练数据中得到相同的经验均值来归一化。

对于一般图像，我们就是做零均值化的预处理。

Weight Initialzation

Xavier初始化

https://zhuanlan.zhihu.com/p/72374385

Batch Normalization（批归一化）

知乎 Batch Normalization原理与实战

避免激活函数饱和

每批是D维的，我们将对每个维度独立计算经验均值和方差，所以基本上每个特征元素通过批量处理我们都计算过了，并对其进行归一化。

训练流程

1. 数据零均值处理

2. 选择架构

3. double check the loss is reasonable：

4. 开始训练：

   a. 从小数据集开始，看是否可以过拟合loss = 0，正确率为1。

   b. 现在可以拿出所有的训练数据，加上一个小的正则化项，确定下什么才是最优的学习率（首先要确定的超参数）。一般范围是1e-3~1e-5。

   c. Hyperparameter Optimization

   Cross_validation strategy

   Random Search vs.Grid Search

更好地优化

再解释一遍BN

从左图上看，如果数据没有被中心化，而且距离坐标系原点很远。我们虽然仍然可以用一条直线（如图所示）分离它们，但是现在如果这条直线稍微转动一点。那么我们的分类器将会被完全破坏。意味着左边例子中的损失函数对于我们权重矩阵中的线性分类器中的小扰动非常敏感。这会使得学习非常困难，因为它们的损失对我们的参数向量非常敏感。

而在使用数据集时，将数据点移动到原点附近并缩小他们的单位方差，我们仍然可以很好的对这些数据进行分类。但是现在当我们稍微的转动直线，我们的损失函数对参数值中的小扰动就不那么敏感了，优化更容易。

超参数搜索

随机搜索：当你的模型性能对某一个超参数对比其他超参数更敏感的时候，随机搜索可以对超参数空间覆盖的更好。

粗细粒交叉搜索（coarse to fine）：当你做超参数优化的时候，一开始可能会处理很大的搜索范围，几次迭代后，就可以缩小范围，圈定荷氏的超参数所在的区域。然后再对这个小范围重复这个过程。

优化问题

SGD

在多维问题上比起局部极小值点，鞍点是个大问题：

在一亿个维度空间中，鞍点意味着在当前鞍点上，某些方向损失会增加，某些方向损失会减小，如果有一亿个维度，它会发生得更加频繁。基本上在任何点上都会发生，然而在局部极小值点上。向一亿个方向中任何一个方向前进损失都会变大，在考虑多维问题上，这种情况非常稀少。

SGD+Momentum

Nseterov动量：

先取得速度方向得步进，之后评估这个位置（经过速度步进后得到的点）的梯度，然后回到原始点，将两者混合起来。

为什么这样做：

如果速度方向有一点作物，那它可以让你在目标函数得高等轮廓图更大一点得部分中加入梯度信息。

AdaGrad

1
2
3
4
5

grad_squared = 0
while True:
    dx = compute_gradient(x)
    grad_squared += dx * dx
    x -= learning_rate * dx/(np.sqrt(grad_squared) + 1e-7)

在优化过程中，需要保持一个在训练过程中的每一步的梯度的平方和的持续估计。

与速度项不同的是，现在我们有了一个梯度平方项。在训练时，我们会一直累加当前梯度的平方到这个梯度的平方项。当我们在更新我们的参数向量时，我们会除以这个梯度平方项。那么现在的问题是这样的缩放，对于矩阵中条件数很大的情形有什么改进呢？

如果我们有两个轴其中一个轴我们有很高的梯度，而另外一个轴方向却有很小的梯度。那么随着我们我们累加小梯度的平方，我们会在最后更新参数向量时候除以一个很小的数字，反而加速了小梯度维度上的学习速度。在另外一个维度方向上，由于梯度变得特别大，我们会除以一个特别大的数，所以我们会降低这个维度方向上的训练速度。

当时间越来越大的时候，在训练过程中使用AdaGrad会发生什么？

使用了Adagrad，步长会变得越来越小。因为随着时间更新梯度平方的估计值，所以这个估计值随着时间单调递增。

当函数是非凸的时候会陷入局部极值

RMSProp

1
2
3
4
5

grad_squared = 0
while True:
    dx = compute_gradient(x)
    grad_squared = decay_rate* grad_squared+（1 - devay_rate）* dx *dx 
    x -= learning_rate * dx/(np.sqrt(grad_squared) + 1e-7)

在RMSProp中仍计算梯度的平方，但是不仅仅在训练中累加梯度平方。而是我们会让平方梯度按照一定比率下降。

Adam

1
2
3
4
5
6
7

first_moment = 0
second_moment = 0
while True:
    dx = compute_gradient(x)
    first_moment = beta1 * first_moment + (1 - beta1) * dx # Momentum
    second_moment = beta2 * second_moment + (1 - beta2)* dx * dx # AdaGrad/RMSProp
    x - = learning_rate * first_moment/(np.sqrt(second_moment) + 1e-7)# daGrad/RMSProp

在最初的一步，在开始时，我们已经将第二动量初始化为0，第二动量经过第一步更新后，仍然非常非常接近于0，现在我们在这做出更新步骤除以第二动量，也就是一个非常小的数，会得到一个非常大的步长。

Adam算法也增加了偏置矫正项，来避免出现开始时得到很大步长。

1
2
3
4
5
6
7
8
9

first_moment = 0
second_moment = 0
for t in range(num_iterations):
    dx = compute_gradient(x)
    first_moment = beta1 * first_moment + (1 - beta1) * dx # Momentum
    second_moment = beta2 * second_moment + (1 - beta2)* dx * dx # AdaGrad/RMSProp
    first_unbias = first_moment / (1 - beta1**t)
    second_unbias = second_moment / (1 - beta2**t)
    x - = learning_rate * first_unbias/(np.sqrt(second_unbias) + 1e-7)# daGrad/RMSProp

我们更新了第一和第二动量之后，我们构造了第一和第二动量的无偏估计。通过使用当前时间步t。现在我们实际上在使用无偏估计来做每一步更新，而不是初始的第一和第二动量估计值

学习率下降

带动量SGD的学习率衰减很常见，但是像Adam的优化算法就很少用学习率衰减。

二阶优化

L-BFGS

在风格迁移里面用到：这个问题有很少地随机性，而且参数也很少，但是仍然是一个优化问题。

之间说过的所有算法都是一阶优化算法。

二阶逼近没有学习率（原始版本）

二阶逼近对深度学习来说有点不切实际，因为这个海森矩阵是N*N的，其中N表示网络中的参数的数量。

通常使用拟牛顿法，而不是牛顿法。不是直接地去求完整地Hessian矩阵地逆，而是去逼近（常用低阶逼近）这个矩阵地逆。

减少训练误差和测试误差之间的差距。

模型集成 ：

正则化

迁移学习

深度学习软件

CNN框架

循环神经网络

识别和分割

目标检测和图像分割

可视化和理解

生成模型

深度增强学习

深度学习方法、硬件对抗样本和训练

网络介绍资讯

MMYOLO

1. MMYolo

   yolo v8 原理核实现全解析

2. MMYOLO保姆级教程