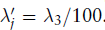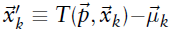配准算法之 — NDT
超级详细介绍NDT
建议下载下来用Typora软件阅读markdown文件
NDT配准算法详解
论文:
The Three-Dimensional Normal-Distributions Transform
– an Efficient Representation for Registration, Surface Analysis, and Loop Detection
作者:
Martin Magnusson
用于表示表面的概率密度函数
- 点云由深度传感器等获取的一组来自表面的空间采样点。使用点云来表示表面有许多限制。例如,点云不包含关于表面特征(如方向、平滑度或孔)的明确信息。1.根据传感器的配置,点云也可能是低效的,需要不必要的大量存储。2.为了在远离传感器位置的地方获得足够的样本分辨率,通常有必要对传感器进行配置,以便从传感器附近的表面产生大量冗余数据。(离传感器远的地方单位体积内点云密度小,离传感器近的地方单位体积内点云冗余)
- 正态分布变换可以描述为一种紧表示曲面的方法。首被Biber和Straßer在2003年作为二维扫描注册方法而提出。
- 该变换将点云映射到光滑的表面表示,该表面表示为一组局部概率密度函数(PDFs),每一个PDFs都描述了表面的一段形状。
PDFs:
PDF的几何意义
正态分布给出了具有连续导数的点云的分段光滑表示。每个PDF都可以看作是局部表面的近似,描述了表面的位置以及它的方向和平滑度。二维激光扫描及其对应的正态分布如图6.1所示。图6.2展示了矿井巷道扫描的三维正态分布。
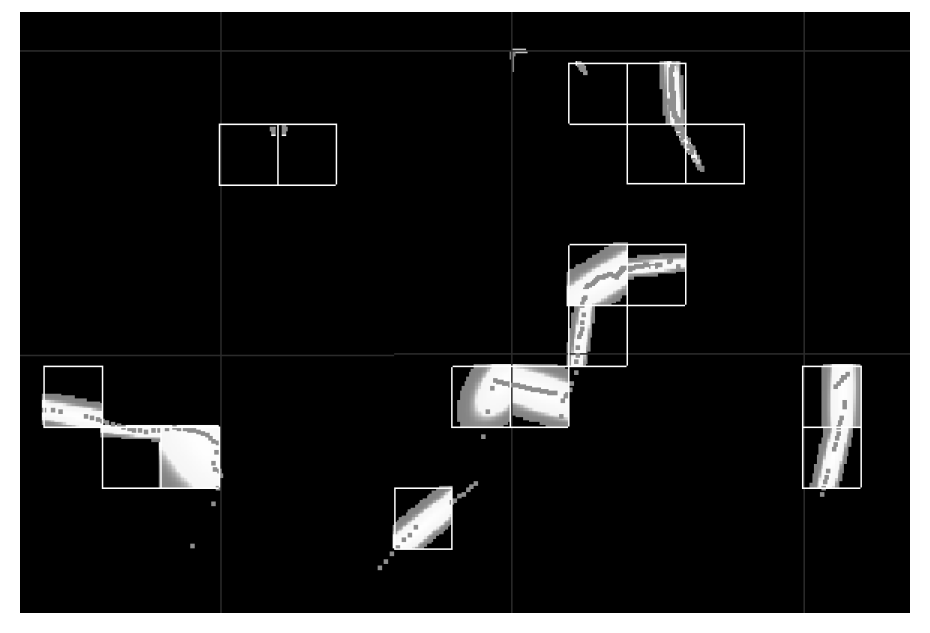
一个二维激光扫描从一个矿井隧道(显示为点)和PDFs描述的表面形状。在这种情况下,每个单元格都是一个边长为2米的正方形。较亮的区域表示较高的概率。PDFs只计算了五点以上的单元格

上图为隧道断面的3D-NDT表面表示。
更亮、更密集的部分表示更高的概率。cell的边长为1米。
单变量和多变量正态分布的特征
- 在一维情况下,对于一个正态分布随机变量x来说,有确定的期望值:μ
和还不确定方差的值:σ。
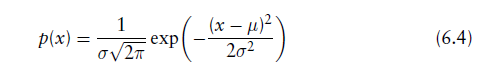
在式子6.1中的多元概率函数 ,在一维情况下(D = 1)降为上面的p(x)。
,在一维情况下(D = 1)降为上面的p(x)。
在多维的情况下,均值μ和方差σ取而代之的是均值向量和协方差矩阵 。
。
协方差矩阵的对角线元素表示每个变量的方差,非对角元素表示变量的协方差。图6.3说明了一维、二维和三维的正态分布。
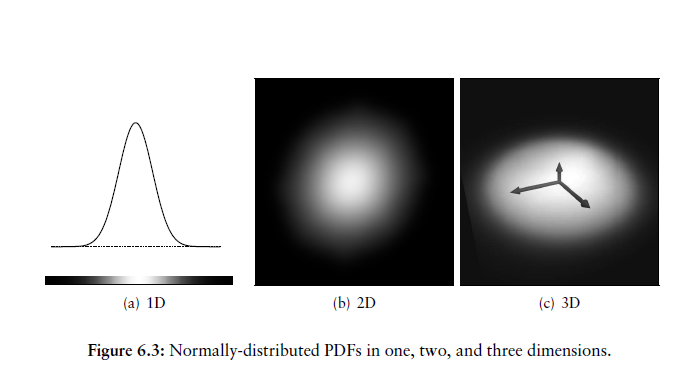
在二维和三维的情况下,可以通过协方差矩阵的特征向量和特征值来判断曲面的方向和光滑度,也就是说,一组正交向量对应于各变量协方差的主方向。取决于方差的比例,二维正态分布可以是点形(如果方差相似),也可以是线形(如果一个比另一个大得多),或者介于两者之间。
在三维情况下如图6.4所示
- 正态分布可以描述点或球(如果方差的大小在各个方向上是相似的),
- 一条直线(如果一个方向的方差远大于另两个方向的方差),
- 或者一个平面(如果一个方向的方差比另两个方向的方差小得多)。

计算每个网格里面的PDF
- 该算法的第一步是将扫描占用的空间细分为单元格网格(a grid of cells)(二维情况下为正方形case,三维情况下为立方体cubes)。
- 根据单元内的点分布,每个单元计算一个PDF。(probability density functions)概率密度函数
每个单元中的PDF可以解释为单元内表面点
的生成过程(generative process)。换句话说,我们假设
的位置是由这个分布生成的。
假设参考扫描表面点的位置是由d维正态随机过程产生的,则该cell中的,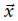 的概率为
的概率为
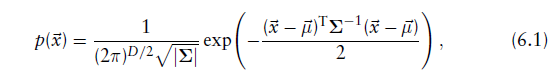
 :该cell中的均值向量(mean vector)和协方差矩阵(covariance matrix)
:该cell中的均值向量(mean vector)和协方差矩阵(covariance matrix)
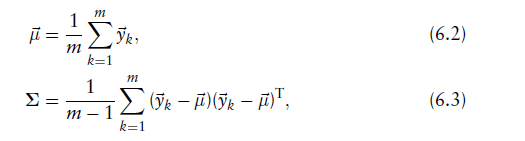
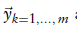 是在cell中的参考表面点集(reference scan points)的位置(positions)
是在cell中的参考表面点集(reference scan points)的位置(positions)
- 分母
 作用:缩放函数使其积分为1,在实际应用中,可以用常数c0替换它。
作用:缩放函数使其积分为1,在实际应用中,可以用常数c0替换它。
NDT配准算法
当你使用NDT算法用于点云配准时,目的是为了找到一个位姿pose(要最优化的对象)—>可以最大化current scan的点位于reference scan表面的可能性。—>maximises the likelihood(目标函数).
a.要优化的参数: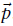
要优化的参数:R, t。即对the current scan的位姿估计的旋转和平移,可以用向量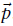 来表示这个参数。
来表示这个参数。
b.输入
- current scan’s points:被表示为一个点云
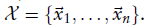 。假设存在一个空间变换函数
。假设存在一个空间变换函数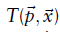 ,通过位姿
,通过位姿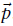 来移动
来移动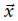
- 给定的一些scan points的PDF
 ,应该找到一个最好的位姿
,应该找到一个最好的位姿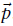 使得下面的似然函数(极大似然函数)最大。
使得下面的似然函数(极大似然函数)最大。
c.两种目标函数
1.极大似然估计(最大化)
- 对点云通过变换函数变换后,对新的点云中每个点的概率累乘
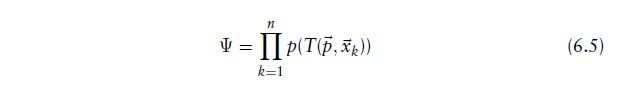
2.负对数似然估计(最小化)
或者可以找到一个最好的位姿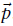 使得化负对数似然函数最小
使得化负对数似然函数最小
- 对点云通过变换函数变换后,对新的点云中每个点的概率的负对数累加
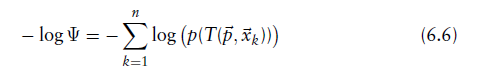
d.改进PDF
如图6.5所示比较正态分布 和混合模型
和混合模型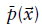 。
。
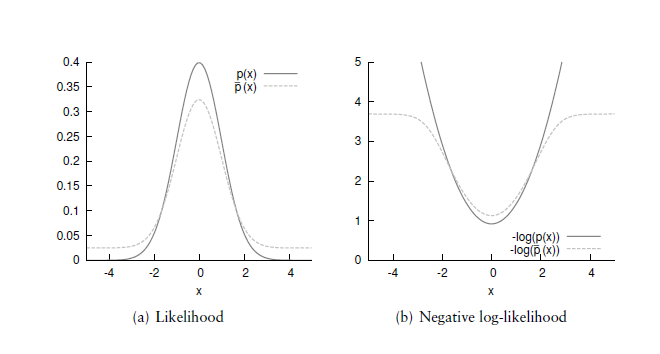
负对数似然是进行NDT扫描配准时的“目标函数”。
它的导数描述了特定测量对解的偏置。(Its derivative characterises the bias that a particular measurement has on the solution.)
对于
,对于较大的
,影响是没有边界的,而对于
,影响是有边界的。
1.使用正态分布和均匀分布的混合模型的PDF: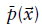
PDF(概率密度函数)不一定限于正态分布,任何局部捕获表面点结构并对异常值具有鲁棒性的PDF都是合适的。
“正态分布的负对数”可能性在远离均值的点上无限增长。
因此,扫描数据中的异常值可能对结果有很大的影响。
在这项工作中(Biber,Fleck,和Straßer 的论文中)采用的是正态分布和均匀分布的混合模型:
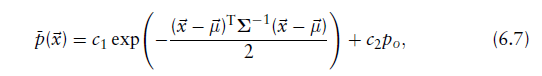
po是异常值的期望比率,利用这个函数
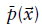 ,异常值的影响是有界的。
,异常值的影响是有界的。常量c1和c2可以通过”在一个单元格所张成的空间内,让
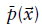 的“概率质量等于1”来确定。
的“概率质量等于1”来确定。概率质量函数:
mass强调的是一个聚集在一起的物体,就是它一个块一块的。这和离散型数据很像,就是一
数据属于某个类。他们是聚集一块一块的。所以用mass这个词来描述他们的概率。翻译成中
就变成了概率质量函数。你可以这么记忆:离散型数据是块状物体,物体是有质量,所以叫
概率质量函数。概率密度函数(Probability Density Function)
这个是描述连续性数据。就是落在某个区间内的概率多大。这个就像液体,液体是连续的。同等体积有些液体重有些液体轻,用密度这个词描述会更合适。它的缩写很意思,叫做PDF,哈哈哈
- 要优化的对数似然能量函数的和由具有这种形式的项组成(要优化的对数似然估计由这样的项相加)
 它们没有简单的一阶和二阶导数。下面提供解决思路。
它们没有简单的一阶和二阶导数。下面提供解决思路。
2.将目标函数近似为高斯函数(负对数似然函数拟合成高斯函数)
由于“要优化的对数似然函数”没有简单的一阶和二阶导数,这样子目标函数优化起来很难,将改进的正态分布和均匀分布的混合近似看作高斯分布,然而,图6.5 b表明对改进的数似然函数(目标函数)可以近似为一个高斯函数。
一个这样的函数:
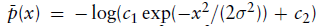 ,
,
可以近似为高斯函数: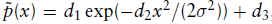
拟合参数
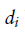 通过
通过
分别让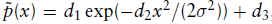 应该像
应该像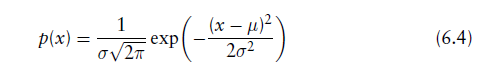
中
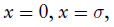 还有
还有 来获得。
来获得。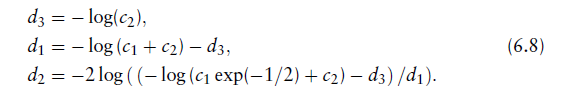
3.最终的目标函数:
对多维的”混合模型的分布“构造的负对数似然函数(目标函数)用高斯函数来近似,来作为目标函数,来对参数(位姿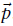 )进行优化。
)进行优化。
a.目标函数的项:
利用这种高斯近似,得到了一个current scan point 对*NDT score function *的影响
对*NDT score function *的影响
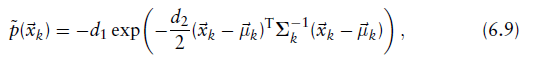
分别代表网格中
在网格中所在位置的均值和协方差
这个NDT score function的导数比6.7式正态分布和均匀分布的混合的导数要简单(优化起来更简单),但在优化时仍然具有相同的一般性质(功能相同但是更加简单)。
d3项在公式6.9中被省略了。当使用NDT进行扫描配准时,这不是必需的,因为它只向score函数添加一个常量偏移量,并且不改变其形状或优化参数。
b.score function(目标函数):
给定一组点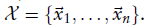 和一个变换函数
和一个变换函数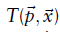 用来通过一个位姿
用来通过一个位姿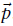 变换每个点
变换每个点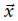 。
。
the current parameter vector的NDT评分函数为: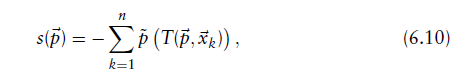
- 该函数表示通过位姿
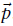 变换点集
变换点集 (k=1~n)到the reference scan上对应的新的点集计算出的似然值(the likelihood)。
(k=1~n)到the reference scan上对应的新的点集计算出的似然值(the likelihood)。
似然函数需要求协方差矩阵的逆矩阵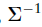。如果网格中的点是完全共面或共线的,协方差矩阵是奇异的,不可逆。在三维情况下,由三个或更少的点计算的协方差矩阵总是奇异的,
因此,PDFs只计算包含5个以上点的单元格。
此外,作为对数值问题的预防,当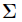被发现几乎是奇异时,它就会轻微地膨胀。如果最大的特征值
比
还要大100被以上,然后是较小的特征值
被设成
然后更新矩阵为: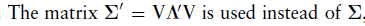
 中包含的特征向量,
中包含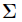的特征向量,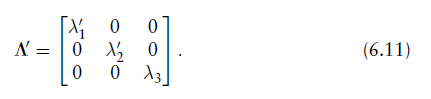
e.使用牛顿法对目标函数进行优化
牛顿算法可以用来求使评分(目标)函数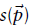 最优化的参数
最优化的参数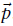
牛顿法迭代地解等式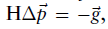
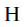 是海森矩阵
是海森矩阵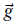 是
是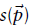 的梯度向量
的梯度向量- 在每次迭代中,将增量
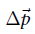 (牛顿方向)添加到当前的位姿估计中以计算出下一次迭代的参数
(牛顿方向)添加到当前的位姿估计中以计算出下一次迭代的参数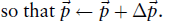
1.计算点云变换后在该cell中的去质心坐标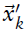
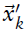 是“
是“ 通过位姿参数变换后得到的新的坐标”减去”所在网格的测点的均值“。
通过位姿参数变换后得到的新的坐标”减去”所在网格的测点的均值“。
2.梯度向量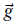 的元素(分量)
的元素(分量) 可以写成
可以写成
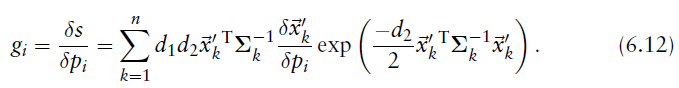
3.海森矩阵中的元素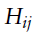
海森矩阵中的元素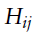 这样计算:
这样计算: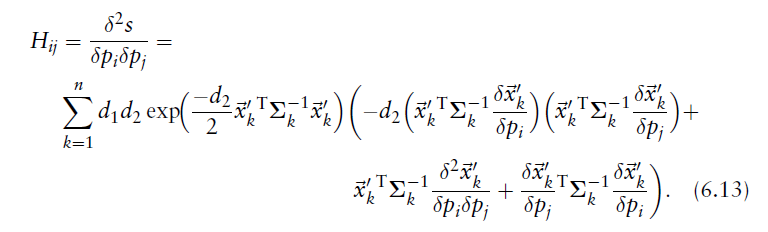
NDT 的score function中的“式子6.12的梯度”,和“式子6.13中的海森矩阵”,无论配准是在2D还是3D(或任何其他维度)中执行,函数都以相同的方式表示。它们同样独立于正在使用的转换表示。
对于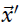 在式子6.12和6.13中的一阶和二阶偏导数来说,它依赖于变换函数T。T可以是2D变换也可以是3D变换
在式子6.12和6.13中的一阶和二阶偏导数来说,它依赖于变换函数T。T可以是2D变换也可以是3D变换
f.以前文章使用的目标函数也可行
在之前的几篇关于NDT扫描配准的文章中[7,48,57,64,67,89],
score function( 目标函数)是直接使用高斯形式的正态分布的PDFs之和来定义的!!!,虽然从概率的角度来看,这样的公式不太令人满意,但是最终的结果与使用混合模型的对数似然的高斯近似(6.9)的结果非常相似(6.7)。
算法流程
算法2描述了如何使用NDT注册(配准)两个点云X和Y。

初始化工作:
- 划分网格,找出参考点云Y的所有点对应的网格
- 对于每个网格计算网格中的参数
- 计算网格中分布的参考点云的点的去质心坐标
- 计算网格中参考点云的去质心坐标的平均值
- 计算网格中参考点云的去质心点的协方差
配准工作:
第一步判断是否收敛
当还没有收敛时,将目标函数,梯度,海森矩阵设为0
第二步对源点集进行相关计算
- 对于源点集中的所有点应用变换矩阵后,这些点坐落在“找到之前划分的网格”的位置
- 计算每个点的高斯近似目标函数的分数,将每个网格中的分数加起来
- 使用公式6.12更新梯度
- 使用公式6.13更新Hessian矩阵
第三步,计算牛顿方向,然后计算出下一个优化矩阵,然后跳到第一步。